多表代换密码原理

多表代换密码首先将明文M分成由n个字母构成的分组$M_1,M_2,\cdots ,M_j$,

对每个分组的$M_i$的加密为：

其中，（A，B）是密钥，A是n X n 的可逆矩阵，满足gcd（|A|，N）= 1,

B = $(B_1,B_2,\cdots,B_n)^T$, C = $(C_1,C_2,\cdots,C_n)^T$, $\mathbf{M}_i$ = $(m_1,m_2,\cdots,m_n)^T$.

对每个分组的$C_i$的解密为：

例如：

加密过程：

n = 3, N = 26

message： you ……（此处就只举例第一个分组了）

you —-> $\mathbf{M}_1$ = $\begin{pmatrix}
24 \
14 \
20
\end{pmatrix}$ , $\mathbf{C}_1$ = $\mathbf{A}$ $\begin{pmatrix}
24 \
14 \
20
\end{pmatrix}$ = $\begin{pmatrix}
22 \
6 \
8
\end{pmatrix}$ . 我们可以知道22，6，8对应的是W，G，I. 加密就此完成。

解密过程：

解密时，先求出

再求：$\mathbf{M}_1$ = $\mathbf{A}^{-1}$ $\begin{pmatrix}
22 \
6 \
8
\end{pmatrix}$ = $\begin{pmatrix}
24 \
14 \
20
\end{pmatrix}$ . $\begin{pmatrix}
24 \
14 \
20
\end{pmatrix}$ —->you. 至此，解密完成。

代码部分：

引入numpy库

1
import numpy as np

将明文进行分组处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def process_text(init_message, group_len):
    """ 将文本进行分组处理 """
    # 去除文本中的空格
    init_message = init_message.replace(" ", "")

    # 计算需要补充的字符数(当明文长度不能被分组长度整除时)
    blank = len(init_message) % group_len

    # 如果有分组长度不足，则补充字符 'z' 直到长度能够整除 group_len
    if blank != 0:
        init_message = init_message + (group_len - blank) * "z"

    # 将字符串转换为小写，并将每个字符转换为对应的 ASCII 码减去 97
    init_message_list = list(init_message.lower())
    code_list = [ord(i) - 97 for i in init_message_list]

    # 将 code_list 按照 group_len 进行分组
    code_group = []
    for i in range(0, len(code_list), group_len):
        code_group.append(code_list[i:i + group_len])

    return code_group

拓展欧几里得算法

1
2
3
4
5
6
7
8
9
10
11
def extended_gcd(a, b):
    """扩展欧几里德算法
    接受两个整数 a 和 b 作为输入，并返回它们的最大公约数（GCD），以及满足 ax + by = gcd(a, b) 的系数 x 和 y。
    """
    if b == 0:
        return 1, 0
    else:
        x, y = extended_gcd(b, a % b)
        x, y = y, x - (a // b) * y
        return x, y
# 该函数也用于在 modular_inverse_element 函数中找到模反元素。

求乘法逆元

1
2
3
4
5
6
7
8
def modular_inverse_element(a: int, m=26):
    """求整数a关于1模m的乘法逆元"""
    # 首先检查 a 和 m 是否互质 若不互质则返回-1
    if (np.gcd(a, m) != 1): return -1
    # 使用 extended_gcd 函数找到满足 a * inv_a + m * _ = 1 的系数 inv_a 和 _
    inv_a, _ = extended_gcd(a, m)
    inv_a %= m
    return inv_a

加密计算

1
2
3
4
5
6
7
8
9
def polyalphabetic_substitution(code: list, A, B, m=26) -> list:
    """加密计算函数"""
    group_len = len(B)  # 获取密钥B的长度作为分组长度
    code = np.mat(code).reshape(group_len, 1)  # 将code转换为矩阵，并调整形状为(group_len, 1)
    C = ((np.dot(A, code)) % m).reshape(-1)  # 使用矩阵乘法和取模运算，计算加密后的结果C
    # C = ((np.dot(A, code) + B) % m).reshape(-1)  # 如果需要加上密钥B，则取消注释此行（但好像有点问题，暂时还没进行修改）
    C = C.tolist()[0]  # 将结果C转换为列表形式
    
    return C

矩阵的乘法逆元

1
2
3
4
5
6
7
8
9
10
11
def modular_inverse_matrix(A, m=26):
    """求矩阵A关于1模m的乘法逆元"""
    detA = np.linalg.det(A)  # 计算矩阵A的行列式
    inv_a = np.linalg.inv(A)  # 计算矩阵A的逆矩阵
    Adjoint = detA * inv_a  # 计算矩阵A的伴随矩阵

    inv_detA = modular_inverse_element(round(detA), m)  # 计算行列式detA关于1模m的乘法逆元
    cipher_inv_a = ((inv_detA % m) * Adjoint) % m  # 计算矩阵A关于1模m的乘法逆元
    cipher_inv_a = np.round(cipher_inv_a).astype(int)  # 将结果四舍五入并转换为整数类型

    return cipher_inv_a  # 返回矩阵A关于1模m的乘法逆元

解密计算

1
2
3
4
5
6
7
8
9
10
def inverse_polyalphabetic_substitution(code: list, inv_a, B, m=26) -> list:
    """解密计算函数"""
    group_len = len(B)  # 获取密钥B的长度
    code = np.mat(code).reshape(group_len, 1)  # 将code转换为矩阵，并调整形状为(group_len, 1)

    M = (np.dot(inv_a, (code)) % m).reshape(-1)  # 解密计算，使用矩阵乘法和取模运算
    # M = (np.dot(inv_a, (code - B)) % m).reshape(-1)  # 如果需要减去密钥B，则取消注释此行（但好像有点问题，暂时还没进行修改）
    M = M.tolist()[0]  # 将结果M转换为列表形式

    return M

加密函数

1
2
3
4
5
6
7
8
9
10
11
12
def encrypt_message(key_a, key_b, plaintext):
    """ 加密函数 """
    ciphertext = ""
    code_group = process_text(plaintext, len(key_b))

    for group in code_group:
        group = polyalphabetic_substitution(group, key_a, key_b)
        group = [chr(i + 97) for i in group]  # 将数字转换为对应的字母
        group = ''.join(group)  # 将列表中的字母连接成字符串
        ciphertext = ciphertext + group + " "

    return ciphertext

解密函数

1
2
3
4
5
6
7
8
9
10
11
12
13
def decrypt_message(key_a, key_b, ciphertext):
    """ 解密函数 """
    plaintext = ""
    code_group = process_text(ciphertext, len(key_b))
    key_a_inv = modular_inverse_matrix(key_a, m=26)

    for group in code_group:
        group = inverse_polyalphabetic_substitution(group, key_a_inv, key_b)
        group = [chr(i + 97) for i in group]  # 将数字转换为对应的字母
        group = ''.join(group)  # 将列表中的字母连接成字符串
        plaintext = plaintext + group + " "

    return plaintext

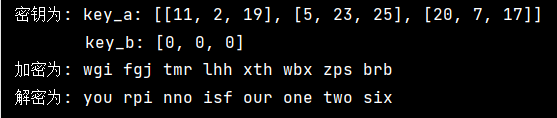
实验测试

1
2
3
4
5
6
7
8
9
10
11
12
if __name__ == '__main__':
    keyA = [[11, 2, 19],
            [5, 23, 25],
            [20, 7, 17]]
    keyB = [0, 0, 0] # 这里B不为0时可能结果有错，暂时还未更改。

    plaintext = "your pin no is four one two six"
    ciphertext = "wgi fgj tmr lhh xth wbx zps brb"

    print("密钥为:", "key_a:", keyA, "\n\t  ", "key_b:", keyB)
    print("加密为:", encrypt_message(keyA, keyB, plaintext))
    print("解密为:", decrypt_message(keyA, keyB, ciphertext))

多表代换运行结果

相关numpy库中函数的用法补充

numpy.mat( )

numpy.mat() 的主要作用是将输入解释为矩阵。与 numpy.array() 不同，numpy.mat() 会返回一个二维矩阵，而不是一个 n 维数组。
例如，如果你有一个列表 [1, 2, 3]，你可以使用 numpy.mat() 将其转换为一个 1x3 的矩阵：

1
2
3
4
5
6
import numpy as np

list1 = [1, 2, 3]
matrix1 = np.mat(list1)

print(matrix1)

运行上述代码，你会得到以下输出：

1
[[1 2 3]]
numop.dot( )

numpy.dot函数用于计算两个数组的点积（内积）。
点积是指两个数组的对应元素相乘后再求和的结果。它可以用于计算向量的长度、计算矩阵的乘法等。
numpy.dot函数的语法如下：

1
numpy.dot(a, b, *out*=None)

其中，a和b是要计算点积的两个数组，可以是一维数组、二维数组或多维数组。out参数是可选的，用于指定计算结果的输出数组。
以下是一些示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

result = np.dot(a, b)
print(result)  # 输出：32

c = np.array([[1, 2], [3, 4]])
d = np.array([[5, 6], [7, 8]])

result = np.dot(c, d)
print(result)  # 输出：[[19 22]
              #        [43 50]]

在这些示例中，np.dot(a, b)计算了一维数组a和b的点积，结果为32。np.dot(c, d)计算了二维数组c和d的点积，结果为一个二维数组.

numpy.reshape( )

numpy.reshape()函数用于改变数组的形状，即重新排列数组的维度。它接受一个数组作为输入，并返回一个具有新形状的数组，而不改变原始数组的数据。
numpy.reshape()函数的语法如下：

1
numpy.reshape(array, newshape, order='C')

参数说明：

  • array：要改变形状的数组。
  • newshape：新的形状，可以是一个整数或一个整数元组。
  • order：可选参数，指定数组在内存中的存储顺序。默认为’C’，表示按行存储。
    下面展示一些示例：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    import numpy as np

    # 创建一个一维数组
    arr = np.array([1, 2, 3, 4, 5, 6])

    # 将一维数组转换为二维数组
    new_arr = np.reshape(arr, (2, 3))
    print(new_arr)
    # 输出:
    # [[1 2 3]
    #  [4 5 6]]

    # 创建一个二维数组
    arr2 = np.array([[1, 2, 3], [4, 5, 6]])

    # 将二维数组转换为三维数组
    new_arr2 = np.reshape(arr2, (2, 3, 1))
    print(new_arr2)
    # 输出:
    # [[[1]
    #   [2]
    #   [3]]
    #
    #  [[4]
    #   [5]
    #   [6]]]

    全部代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
import numpy as np

def process_text(init_message, group_len):
    """ 将文本进行分组处理 """
    # 去除文本中的空格
    init_message = init_message.replace(" ", "")

    # 计算需要补充的字符数(当明文长度不能被分组长度整除时)
    blank = len(init_message) % group_len

    # 如果有分组长度不足，则补充字符 'z' 直到长度能够整除 group_len
    if blank != 0:
        init_message = init_message + (group_len - blank) * "z"

    # 将字符串转换为小写，并将每个字符转换为对应的 ASCII 码减去 97
    init_message_list = list(init_message.lower())
    code_list = [ord(i) - 97 for i in init_message_list]

    # 将 code_list 按照 group_len 进行分组
    code_group = []
    for i in range(0, len(code_list), group_len):
        code_group.append(code_list[i:i + group_len])

    return code_group


def extended_gcd(a, b):
    """扩展欧几里德算法
    接受两个整数 a 和 b 作为输入，并返回它们的最大公约数（GCD），以及满足 ax + by = gcd(a, b) 的系数 x 和 y。
    """
    if b == 0:
        return 1, 0
    else:
        x, y = extended_gcd(b, a % b)
        x, y = y, x - (a // b) * y
        return x, y
# 该函数也用于在 modular_inverse_element 函数中找到模反元素。

def modular_inverse_element(a: int, m=26):
    """求整数a关于1模m的乘法逆元"""
    # 首先检查 a 和 m 是否互质 若不互质则返回-1
    if (np.gcd(a, m) != 1): return -1
    # 使用 extended_gcd 函数找到满足 a * inv_a + m * _ = 1 的系数 inv_a 和 _
    inv_a, _ = extended_gcd(a, m)
    inv_a %= m
    return inv_a


def polyalphabetic_substitution(code: list, A, B, m=26) -> list:
    """加密计算函数"""
    group_len = len(B)  # 获取密钥B的长度作为分组长度
    code = np.mat(code).reshape(group_len, 1)  # 将code转换为矩阵，并调整形状为(group_len, 1)
    C = ((np.dot(A, code)) % m).reshape(-1)  # 使用矩阵乘法和取模运算，计算加密后的结果C
    # C = ((np.dot(A, code) + B) % m).reshape(-1)  # 如果需要加上密钥B，则取消注释此行（但好像有点问题，暂时还没进行修改）
    C = C.tolist()[0]  # 将结果C转换为列表形式

    return C

def modular_inverse_matrix(A, m=26):
    """求矩阵A关于1模m的乘法逆元"""
    detA = np.linalg.det(A)  # 计算矩阵A的行列式
    inv_a = np.linalg.inv(A)  # 计算矩阵A的逆矩阵
    Adjoint = detA * inv_a  # 计算矩阵A的伴随矩阵

    inv_detA = modular_inverse_element(round(detA), m)  # 计算行列式detA关于1模m的乘法逆元
    cipher_inv_a = ((inv_detA % m) * Adjoint) % m  # 计算矩阵A关于1模m的乘法逆元
    cipher_inv_a = np.round(cipher_inv_a).astype(int)  # 将结果四舍五入并转换为整数类型

    return cipher_inv_a  # 返回矩阵A关于1模m的乘法逆元

def inverse_polyalphabetic_substitution(code: list, inv_a, B, m=26) -> list:
    """解密计算函数"""
    group_len = len(B)  # 获取密钥B的长度
    code = np.mat(code).reshape(group_len, 1)  # 将code转换为矩阵，并调整形状为(group_len, 1)

    M = (np.dot(inv_a, (code)) % m).reshape(-1)  # 解密计算，使用矩阵乘法和取模运算
    # M = (np.dot(inv_a, (code - B)) % m).reshape(-1)  # 如果需要减去密钥B，则取消注释此行（但好像有点问题，暂时还没进行修改）
    M = M.tolist()[0]  # 将结果M转换为列表形式

    return M

def encrypt_message(key_a, key_b, plaintext):
    """ 加密函数 """
    ciphertext = ""
    code_group = process_text(plaintext, len(key_b))

    for group in code_group:
        group = polyalphabetic_substitution(group, key_a, key_b)
        group = [chr(i + 97) for i in group]  # 将数字转换为对应的字母
        group = ''.join(group)  # 将列表中的字母连接成字符串
        ciphertext = ciphertext + group + " "

    return ciphertext


def decrypt_message(key_a, key_b, ciphertext):
    """ 解密函数 """
    plaintext = ""
    code_group = process_text(ciphertext, len(key_b))
    key_a_inv = modular_inverse_matrix(key_a, m=26)

    for group in code_group:
        group = inverse_polyalphabetic_substitution(group, key_a_inv, key_b)
        group = [chr(i + 97) for i in group]  # 将数字转换为对应的字母
        group = ''.join(group)  # 将列表中的字母连接成字符串
        plaintext = plaintext + group + " "

    return plaintext

if __name__ == '__main__':
    keyA = [[11, 2, 19],
            [5, 23, 25],
            [20, 7, 17]]
    keyB = [0, 0, 0] # 这里B不为0时可能结果有错，暂时还未更改。

    plaintext = "your pin no is four one two six"
    ciphertext = "wgi fgj tmr lhh xth wbx zps brb"

    print("密钥为:", "key_a:", keyA, "\n\t  ", "key_b:", keyB)
    print("加密为:", encrypt_message(keyA, keyB, plaintext))
    print("解密为:", decrypt_message(keyA, keyB, ciphertext))